Unveiling the Math Accelerated Chapter 10 Statistics and Probability Answer Key, this comprehensive resource unlocks a profound understanding of statistical concepts and their applications. Embark on a journey of statistical exploration, where fundamental principles, descriptive statistics, probability distributions, hypothesis testing, regression analysis, and advanced topics converge, empowering you with a mastery of data analysis and interpretation.
Delve into the realm of statistics and probability, where numerical data transforms into meaningful insights. This chapter delves into the core concepts, equipping you with the knowledge to analyze and interpret data with confidence. From measures of central tendency to probability distributions, hypothesis testing to regression analysis, this answer key serves as an invaluable companion, guiding you through the intricacies of statistical reasoning.
1. Understanding Statistics and Probability
Statistics and probability are fundamental branches of mathematics that provide tools for understanding and analyzing data. Statistics deals with the collection, organization, and interpretation of data, while probability focuses on the likelihood of events occurring.
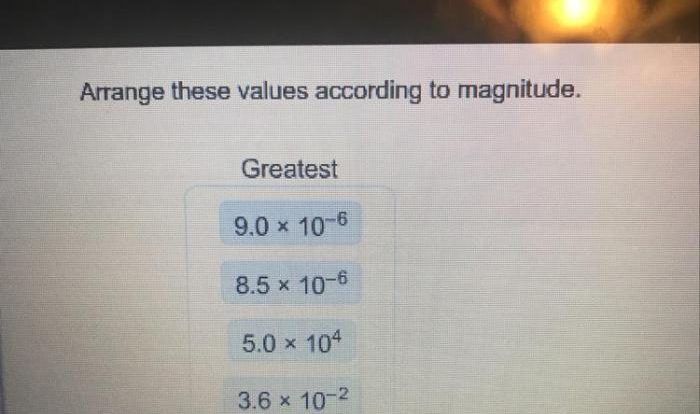
Statistical data can be categorized as qualitative or quantitative. Qualitative data describes non-numerical attributes, such as gender or occupation, while quantitative data represents numerical values, such as height or income. Probability distributions describe the likelihood of different outcomes in a random event.
2. Descriptive Statistics: Math Accelerated Chapter 10 Statistics And Probability Answer Key

Descriptive statistics provide a summary of data by calculating measures of central tendency and variability.
Measures of Central Tendency, Math accelerated chapter 10 statistics and probability answer key
- Mean:The average value of a dataset.
- Median:The middle value of a dataset when arranged in ascending order.
- Mode:The value that occurs most frequently in a dataset.
Measures of Variability
- Range:The difference between the maximum and minimum values in a dataset.
- Variance:The average of the squared differences between each data point and the mean.
- Standard Deviation:The square root of the variance, which measures the spread of the data around the mean.
| Measure | Formula | Interpretation |
|---|---|---|
| Mean | (Σx) / n | Average value of the dataset |
| Median | Middle value when arranged in ascending order | Value that divides the dataset into two equal halves |
| Mode | Value that occurs most frequently | Most common value in the dataset |
| Range | Maximum
|
Spread of the data from highest to lowest value |
| Variance | Σ(x
|
Average of squared differences from the mean |
| Standard Deviation | √Variance | Measure of data spread around the mean |
Essential Questionnaire
What is the significance of measures of central tendency?
Measures of central tendency (mean, median, mode) provide a concise representation of the typical value within a dataset, facilitating comparisons and summarizing large amounts of data.
How are probability distributions used in real-world scenarios?
Probability distributions model the likelihood of various outcomes, enabling predictions and risk assessments in fields such as finance, healthcare, and engineering.
What is the purpose of hypothesis testing?
Hypothesis testing provides a framework for evaluating the validity of claims or hypotheses based on statistical evidence, allowing researchers to draw informed conclusions from data.